[ Introduction | Method | Results | Discussion | Other Observations | Conclusion ]
Introduction
Scientology relies on the e-meter for auditing, which they have
described as a form of "spiritual counselling". Hubbard claims that by
asking a preclear questions and reading their response on the
meter, an auditor is able to find areas of upset in the
preclear's life. Hubbard also claims that the e-meter measures "mental
mass", or energy buildups caused by previous upsets. In yet another
claim, Hubbard states the e-meter reads the "carrier wave" of the thetan
(spirit), and goes on to define its frequency as some ridiculously high
number, on the order of 10^69 Hz.
In actuality, the e-meter is simply a high-precision differential ohmmeter. Changes in the person's resistance are indicated by the meter movement. The auditor adjusts the "Tone Arm" (don't ask...) to center the needle on the dial. The auditor can also adjust the gain of the E-meter amplifier to register only gross changes or every little flinch of the preclear.
It should be noted that a physical meter movement has mass, which according to Newton, resists a change in motion. Because of this, meter movements (and especially large meter movements like the one used in Hubbard's E-meter) are incapable of measuring frequencies beyond a few hertz. This experiment seeks to determine the frequency response of the E-meter.
It should be noted that the low frequency response of the e-meter places
an upper limit on a thetan's "carrier wave". Using Planck's constant,
one can relate frequency to energy. When a "carrier wave" in the 1 Hz
region is related to energy, it can be seen that Hubbard's thetans
possess very little energy indeed; certainly not enough to be "at cause
over Matter, Energy, Space, and Time."
Method
To measure the frequency response of the e-meter, a Wein Bridge
oscillator, oscilloscope, and single-ended power supply were used.
(Ironically, a bridge oscillator is being used to measure a bridge
detector.)
The oscillator uses a TL074 quad op-amp, although only two of the
op-amps are actually used. Op-amps typically require two power
supplies, one positive and one negative. To avoid this expensive
requirement, a "virtual ground" was created for the oscillator at
precisely the midpoint between true ground and the supply voltage. The
first op-amp (U1A) supplies the virtual ground while the second op-amp
(U1B) implements the oscillator.
U1A is configured as a "voltage follower", that is to say its output tracks the voltage on U1A+. The 10-turn pot at U1A+ centers virtual ground at one-half of the input voltage. The U1B- 10-turn pot adjusts the gain of the oscillator. When enough gain exists, a sine wave appears at Output. The two diodes stabilize the oscillator. Oscillation occurs when the reactance of one RC arm is equal to the reactance of the other RC arm, and occurs at a frequency of 1/(2*pi*RC). Due to capacitor and resistor tolerances, frequency will deviate somewhat from the equation. Therefore, frequency is measured directly from the oscilloscope.
The theory behind the Wein Bridge oscillator is beyond the scope of this discussion. For more information, the reader is directed to a college textbook on oscillator theory.
A Dual Trace Storage Oscilloscope was used for this experiment. By storing the waveform, 10 or more cycles can be displayed and a more precise frequency measurement can be obtained. Before each E-meter measurement is taken, the oscillator voltage is precisely controlled to yield an output of 10.0 Volts peak-to-peak (Vpp), +/- .05 volts. The E-meter has 40-50 divisions on its face, so the reading is simply the number of divisions the needle "swings" in response to the standard 10 Vpp signal. The Tone Arm is used to center swinging needle on the meter and to further adjust the lower side of the swing exactly on a division mark.
The E-meter alligator clips hold a 5.6K resistor. Hubbard uses a 4.99K
precision resistor to calibrate the E-meter for females, and 7.50K for
males. Thus, 5.6K is within the specified operating range of the meter.
The oscillator is always set for the same amplitude for each frequency,
in this case 10.0 Vpp Output, which is coupled to the E-meter
with a 150K resistor. This sets the injected current into the E-meter
at 10/150K = 66 ua pp. Oscilloscope ground, power ground, and one side
of the E-meter are tied to a common point.
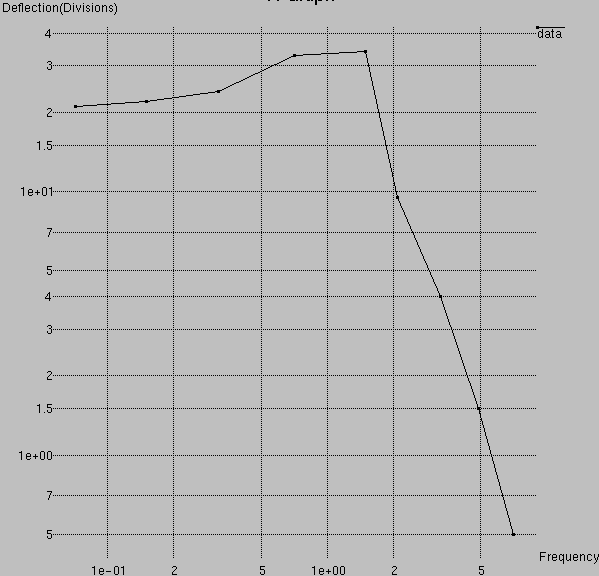
Results
Various resistance values were used to adjust the frequency. Three
measurements per frequency decade were taken, with intermediate
measurements taken when something "interesting" was happening. The
raw data is tabulated below:
freq(Hz) divisions R -------- ---------- ---- .071 31-10 = 21 1.0M .15 32-10 = 22 470K .32 33-9 = 24 220K .71 37-4 = 33 100K 1.5 38-4 = 34 47K 2.1 27-15.5 = 9.5 33K 3.3 23-19 = 4.0 22K 4.9 1.5 15K 7.1 .5 10KFrequency response graphs are typically plotted log10(f) vs 20*log10(V/V0)
Other Observations
When the e-meter probes are placed across a 5.6K resistor, the 'scope
shows a pure DC sampling current. DC is not preferred, because DC will
cause electrolysis, creating a mini "battery" to be formed at the
skin/metal junction which can invalidate the measurement. When AC is
used, this battery is reversed at every cycle, minimizing the effect.
The E-meter has three ferrite toroids to protect it from induced RF
pickup. There are no other frequency-sensitive components in the
detector circuit that would account for the low corner frequency.
Discussion
This curve is immediately recognized by an electrical engineer to be a
classical low-pass filter. The frequency response below 0.2 Hz is
relatively flat.
The "bump" at 1 Hz indicates that the system is underdamped. This is confirmed by Arnaldo Lerma's contention that Hubbard required an underdamped meter movement for "proper" performance. (It should be noted that electrical systems design engineers attempt to achieve what is called critical damping. When a system is critically damped, it will "settle" as quickly as possible. An underdamped system will tend to oscillate after a large step in input, as seen during this experiment.)
Finally, the response rolloff at 2Hz is 9dB in a frequency range of 7.1/2.1 = 3.38. This corresponds to a rolloff of 17.3 dB/decade. The theoretical single-pole rolloff is 20 dB/decade, so this matches well to a graphical determination based on data close to the corner frequency.
Determining the actual corner frequency is done by graphical inspection.
By examining the response curves of other underdamped low-pass filters
with known corner frequencies, professional experience would place the
corner frequency at approximately 1.0 Hz.
Conclusions
Given a lack of any electronic filtering in the 1 Hz range, it is
apparent that the mass of the meter movement is the biggest contributor
to the limited frequency response of the E-meter. Higher frequency
response could be gained by reducing the rotational inertia of the
needle - essentially reducing its mass at the tip, as well as reducing
its overall length. Of course, a modern system would dispense with the
mechanical movement entirely and use an analog-to-digital converter
inside a PC (a.k.a. SoundBlaster), displaying the result
on the computer screen. It is also noted that a fully-loaded PC is
also less expensive than an E-meter and you can even use it
to surf the Web when you're done auditing your buddies.
The underdamped nature of the E-meter will cause certain measurements to look the same. For example, a 1Hz square wave will cause the same motion on the needle as a 1Hz sine wave. In biofeedback terms, a rapid change (square wave) will be smoothed out (sine wave). These two conditions indicate radically different underlying physiological phenomena, so a device which confuses the two is decidedly non-optimal.
The E-meter exhibits the classical frequency response of an underdamped single-pole low pass filter with a corner frequency of approximately 1.0 Hz. Other medical research (EEGs, EKGs, etc) show that bodily processes occur at frequencies several orders of magnitude higher than this. As such, the E-meter is an extremely poor diagnostic tool.
Hubbard's notion of "carrier waves" is pure unadulterated hoakum. The E-meter uses a DC sampling current and the device cannot measure anything beyond 10 Hz. Taken along with its other deficiencies, it is clear that Hubbard's primary use of the E-meter was to lend an air of scientific respectability to an area fraught with psuedoscience.